How to divide larger numbers and do long division?
This is video for how to divide large numbers by doing long division with easy methods. This video describes that dividing the "Dividend" with "Divisor" to get the "Quotient" and "Remainder" if they exist. In the given example first "25" taken as the Dividend and "5" is will be the Divisor. Divide this value the multiplication is needed. For above example "5*5=25" is the result so, the "Quotient" is "5".If the value is large for example "506" of dividend and "8" of divisor means, first we should take the first two digit of the dividend value for division, the value will be "6*8=48". Now, we will get the Quotient of "6" first and the remainder will be "2", now the third digit of the dividend "6" will be suffixed with remainder, now the value will be "26".Then "3*8=24" will be the value for second division. So now finally we will get the "Quotient" as "63" and the "Remainder" as "2".
Basic procedure for long division by longhand
- When dividing two numbers, for example, n divided by m, n is the dividend and m is the divisor; the answer is the quotient.
- Find the location of all decimal points in the dividend and divisor.
- If necessary, simplify the long division problem by moving the decimals of the divisor and dividend by the same number of decimal places, to the right, (or to the left) so that the decimal of the divisor is to right of the last digit.
- When doing long division, keep the numbers lined up straight from top to bottom under the tableau.
- After each step, be sure the remainder for that step is less than the divisor. If it is not, there are three possible problems: the multiplication is wrong, the subtraction is wrong, or a greater quotient is needed.
- In the end, the remainder, r, is added to the growing quotient as a fraction, r/m.
Long division does not use the slash (/) or obelus (÷) signs, instead displaying the dividend, divisor, and (once it is found) quotient in a tableau. An example is shown below, representing the division of 500 by 4 (with a result of 125).
125 (Explanations)
4)500
4 (4 × 1 = 4)
10 (5 - 4 = 1)
8 (4 × 2 = 8)
20 (10 - 8 = 2)
20 (4 × 5 = 20)
0 (20 - 20 = 0)
The process is begun by dividing the left-most digit of the dividend by the divisor. The quotient (rounded down to an integer) becomes the first digit of the result, and the remainder is calculated (this step is notated as a subtraction). This remainder carries forward when the process is repeated on the following digit of the dividend (notated as 'bringing down' the next digit to the remainder). When all digits have been processed and no remainder is left, the process is complete.
Here is an example of the process not producing an integer result:
31.75
4)127
12 (12-12=0 which is written on the following line)
07 (the seven is brought down from the dividend 127)
4
3.0 (3 is the remainder which is divided by 4 to give 0.75)
2.8 (7 × 4 = 28)
20 (an additional zero is brought down)
20 (5 × 4 = 20)
0
In this example, the decimal part of the result is calculated by continuing the process beyond the units digit, 'bringing down' zeros as being the decimal part of the dividend.
This example also illustrates that, at the beginning of the process, a step that produces a zero can be omitted. Since the first digit 1 is less than the divisor 4, the first step is instead performed on the first two digits 12. Similarly, if the divisor were 13, one would perform the first step on 127 rather than 12 or 1.
Source: Wikipedia




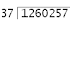





0 comments:
Post a Comment