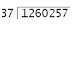Another type of division you’ll encounter is division with decimals in both the divisor and the dividend. It might look something like this:
In this situation, you move the decimal place the number of spaces in the divisor until the decimal is at the end of the number; you move the decimal the same number of spaces in the dividend: this does NOT necessarily mean the decimal will land at the end of the dividend. Here’s an example:
Your new problem looks like this (note the change in decimal places in both the divisor and dividend):
Now you continue to work the problem out, remembering to bring your decimal up into your quotient at the appropriate time (it will be in red in the diagram).
Thus, your final answer is simply 16.
Let’s try one more example of moving the decimal over in order to solve the problem.
becomes
After the decimals are moved, it looks like this:
After you move the decimals, continue the problem, like this:
Thus, your final answer is 6.25.
We’ve already practiced long division, but so far our answers have all come out even (in other words, our last subtraction problem ended in an answer of 0). However, sometimes our division problems will not come out evenly, and we will have another number (not 0) when we do the last subtraction problem. This leftover number is called a
remainder, and it is written as part of the quotient. Follow along with this example:

The red circled number at the bottom our remainder. You do not have to circle the remainder; we just circled ours so that you know which number it is. After you have your remainder, you write it on top of the division bar, with an r in front of it, like this: 25 r 3.
When your division ends with a remainder, you must make sure that your remainder is less than your divisor. If your remainder is more than your divisor, you need to go back and check your division, because it is incorrect. We can still use our multiplication method to check our division; you will multiply the quotient (25) by the divisor (5), and then add our remainder to the answer to the multiplication problem, like this:

Let’s try that one more time. Here’s a new example:

Our answer to this problem is 23 r 1; note that we always write the remainder after the quotient, on top of the division bar. Also notice that our remainder (1) is smaller than our divisor (6).
Now let’s check our work, like this:

There are also several different ways to write remainders. The standard way is shown above, with an r in front of the number. However, you can also write remainders as fractions and as decimals.
Long Division with Remainders as Fractions
Now that you understand the basics of long division, you may be asked to write your remainder as a fraction. Don’t worry! It’s not hard at all. You’re going to do long division the same way—divide, multiply, subtract, bring down, and then you’re going to get a remainder. Instead of writing r and then the number, you are going to take your remainder and make it the numerator of a fraction. The denominator comes from the divisor—you use the same number you’re dividing by in your denominator.
Let’s look at the following example:

Notice that you do not use the r at all in front of your remainder when you’re turning it into a fraction. However, you do still write the fraction as part of the quotient (answer to your division problem).
Also, you would check this division problem the same way as a normal division problem; multiply the quotient (23) by the divisor (6) and then add the remainder (1). Do not do anything with the fraction in order to check this problem.
Long Division with Remainders as Decimals
Another way you may be asked to express a remainder is in the form of a decimal. When you’re asked to express your remainder as a decimal, you first complete division as usual, until you get to the point you usually end at, where you have nothing else to bring down. Instead of stopping here, however, you are going to keep going with division. You will add a decimal point (.) after the last number given in the dividend, and you will also place a decimal point in the quotient after the number you have so far. After the decimal in the dividend, you will add a zero (0) and continue division. You will keep adding zeroes until your subtraction step results in an answer of 0 as well. Follow along with this example:

Notice that we added a decimal after the 6 in the dividend, as well as a decimal after the 5 in our quotient. Then, we started adding zeroes to the dividend. This time, it only took us one added zero before our remainder was zero.
Now, let’s look at a problem where you’d have to add more than one zero to the dividend:

When you have your quotient with a decimal, you check the answer differently than if it had a remainder as a fraction or just a remainder written with r. Instead of adding the remainder separately, you just multiply the quotient (including decimal) by the divisor, like this: